Hoy es el Día Internacional de las Matemáticas (que habitualmente conocíamos como Día de Pi (π)). Para celebrarlo, nuestro profesor del Doble Grado en Matemática Computacional e Ingeniería del Software, Enrique Ferres, te cuenta seis curiosidades del número Pi que tal vez desconozcas. ¡Apunta!
- El Día Internacional de las Matemáticas se lo debemos al número π. Desde hace algunos años lo que se venía celebrando en este día era el Día de Pi, creado por el estadounidense Larry Shaw. La razón es que el 14 de marzo es el 14 del 3, pero en notación anglosajona es el 3/14 (o 3,14), primeras cifras de este número. Por cierto, también es el aniversario del nacimiento de Albert Einstein.
- “π” es la letra del alfabeto griego que representa la “p”. ¿Sabías por qué se utiliza para designar al famoso número? Sabemos que la longitud (perímetro) de una circunferencia de radio r es 2πr, aunque como 2r es el diámetro, que llamaremos d, la longitud de la circunferencia es d. Así, π se define como la proporción que guarda el perímetro de la circunferencia con su diámetro. Por tanto, para una circunferencia de diámetro d = 1, su perímetro es π. π es la primera letra de la palabra griega “περιµετ ρoν”, que significa perímetro. W. Oughtered, I. Barrow o D. Gregory (s. XVII), ya utilizaron esta letra para designar a esta cantidad, pero no fue hasta 1706 que W. Jones (1706) institucionalizara su nombre.
- π = 3,14 o π = 3,1416. ¿Cuántas veces lo hemos escrito? Realmente π es un número irracional, es decir, tiene infinitos decimales no periódicos. Pero, ¿por qué sabemos que “más o menos” vale 3,14? π es, por definición, la proporción que guarda la longitud y el diámetro de una circunferencia. Pero también sabrás que el área de un círculo es πr2 . Por tanto, podemos definir π como la proporción que guardan el área y el cuadrado del radio de un círculo. En verdad, no es trivial que este π y el π del perímetro de la circunferencia sean el mismo, pero bueno, supongamos que ya lo sabemos. π lo podríamos calcular construyendo un círculo de radio 1. Entonces tendríamos que su área sería π. Pero, ¿cómo calcular el área del círculo sin su fórmula? Visitemos la Grecia Clásica para averiguarlo:
Arquímedes, ese gran matemático que hacía arder las velas de los barcos enemigos desde la orilla sin ningún arma (en realidad utilizaba lupas para concentrar los rayos de sol en un solo punto), tiene la respuesta. Dentro del círculo de radio r = 1 construía un triángulo equilátero cuyo centro era el centro del círculo y los vértices se hallaban sobre la circunferencia. Entonces, como todavía sobraba mucha superficie de círculo, construía un cuadrado de la misma forma. Como seguía sobrando mucha superficie de círculo, construía un pentágono, un hexágono, etc. Cuando el polígono de n lados inscrito en el círculo era suficientemente grande, el área se parecía mucho a la del círculo, π. De hecho, ¡una circunferencia es un polígono regular con infinitos lados! Desde el siglo XVII a este proceso se le llama “paso al límite”, y forma parte del cálculo infinitesimal. En la época de los griegos existía algo parecido: el método exhaustivo que ideó Eudoxo de Cnido y del que se valió Arquímedes para hacer muy buenas aproximaciones al valor de π.
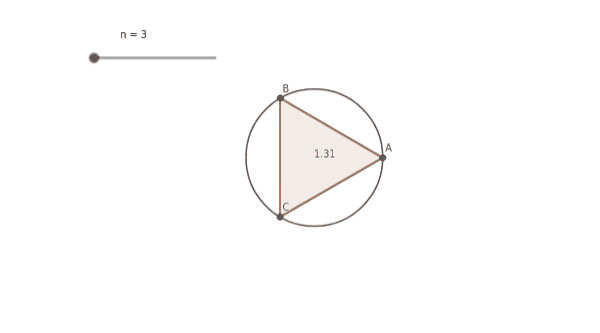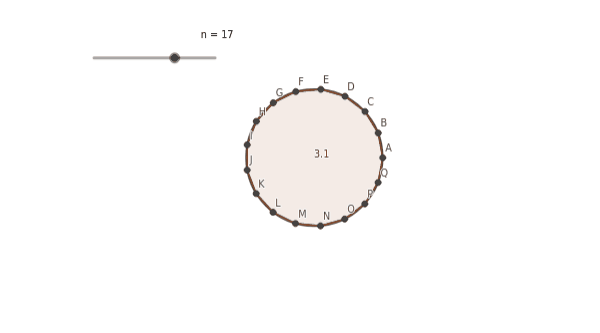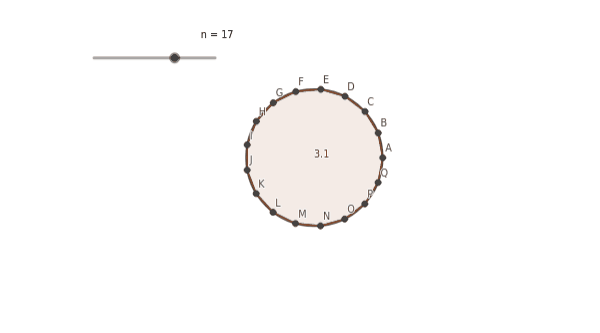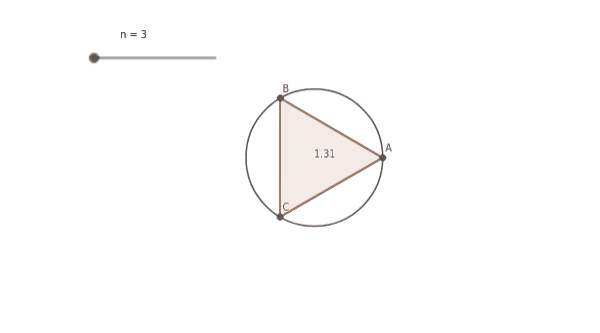
- Un número irracional (de nuevo, infinitos decimales no periódicos) se dice que es un número normal si la frecuencia con la que aparece cada una de las cifras del 0 al 9 en la expresión del número es la misma. Por ejemplo, la constante de Champernowne, 0,1234567891011 . . ., formada por la concatenación de todos los números naturales, es un número normal. Mucho se ha conjeturado sobre si π es un número normal, pero hasta la fecha no se ha podido demostrar. Lo que sí que se sabe es que es un número trascendente, gracias a Lindemann, desde 1882. Los números trascendentes son aquellos que no son solución de ninguna ecuación con coeficientes racionales. Por cierto, que sea trascendente implica la imposibilidad de la cuadratura del círculo, aquel problema planteado por el Oráculo de Delos en la Grecia Clásica que pedía construir un cuadrado cuya área fuese igual a la del círculo, es decir, a π.
- Fue y cayó. Y queda solamente la inútil cifra con pocos destinos poderosos, tristes devenires sin el más sencillo bien. Idiota, re idiota, sabe que sus encantos son ya latosos decimales. Pobre… A este tipo de poemas se los conoce como piemas, y sirven para recordar los decimales de π. En este piema de origen argentino encontramos la secuencia.
3,1415926535897932384626433832795
- π es uno de esos números que mayor misticismo y curiosidad generan, e incluso ha dado título a grandes películas como ‘La vida de Pi’, de Ang Lee, o, una de mis recomendaciones personales: ‘Pi: fe en el caos’, de Darren Aronofsky.
Si te has quedado con ganas de conocer más cosas sobre el número π, te recomiendo la lectura Los secretos del número π, de Joaquín Navarro.
